Usage of the package QuarkConstruction with Mathematica

Make sure you put quarkConstruction.jar onto your CLASSPATH before trying the example below, or use the AddToClassPath feature of J/Link to make it available.

The package defines the following constants.

HO = 0 specifies the type of polyhedra related with family Hexahedron-Octahedron.
DI = 1 specifies the type of polyhedra related with family Dodecahedron-Icosahedron.
RIGHT = 0 specifies the right-handed type of polyhedra.
LEFT = 1 specifies the left-handed type of polyhedra.

To obtain components and characteristics of polyhedra the following methods are determined.

getVertices[] gives a list of the vertex coordinates.
getFaces[] gives a list of the 0-based vertex numbers associated with each face.
getNumVertices[] gives a number of the vertices.
getNumFaces[] gives a number of the faces.

Usage:
mesh[obj_] := Module[{v,f},
v = obj@getVertices[];
AllowRaggedArrays[True];
f=obj@getFaces[] + 1;
AllowRaggedArrays[False];
Polygon[#]& /@ (v[[#]]& /@ f)]
(* gives a list of polygons for a polyhedron *)

The package contains the following classes.

Quarkhedron

Class of polyhedra family.

Constructors

Quarkhedron[type] type = HO or DI, orientation = RIGHT.
Quarkhedron[type, orientation] type = HO or DI, orientation = RIGHT or LEFT.

Usage:
quarkhedronHO = JavaNew["sun4v.qc.Quarkhedron",0];
quarkhedronDI = JavaNew["sun4v.qc.Quarkhedron",1];
Show[GraphicsArray[{Graphics3D[mesh[quarkhedronHO]],
Graphics3D[mesh[quarkhedronDI]]}]];

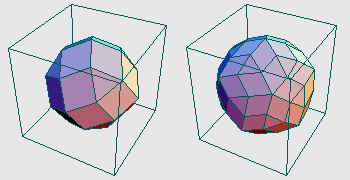
Methods

setValue[numMode, value] sets the value for mode with a 0-based index numMode. Quarkhedron of HO type has 4 modes, of DI type - 5 modes. value >= 0.
setValue[{value0, ..., valueN}] sets values for modes starting from 0 index.
resetValues[] sets values equal 1 for all modes.
setOrientation[orientation] sets the value of the orientation. orientation = RIGHT or LEFT.
setUnitDirection[value] scales a polyhedron and it is applied at parqueting. value > 0. For correct scaling value is extracted at the getUnitDirection[] method of the Modeler class.

Usage:
quarkhedronHO@setOrientation[1];
quarkhedronDI@setOrientation[1];
Show[GraphicsArray[{Graphics3D[mesh[quarkhedronHO]],
Graphics3D[mesh[quarkhedronDI]]}]];

quarkhedronHO@setOrientation[0];
quarkhedronDI@setOrientation[0];
quarkhedronHO@setValue[2,2];
quarkhedronDI@setValue[2,2];
Show[GraphicsArray[{Graphics3D[mesh[quarkhedronHO]],
Graphics3D[mesh[quarkhedronDI]]}]];

Element

Class of polyhedra of family Hexahedron-Octahedron or Dodecahedron-Icosahedron. These polyhedra form a parquet cover for Quarkhedra accordingly HO or DI types.

Constructors

Element[type] type = HO or DI.

Usage:
elementHO = JavaNew["sun4v.qc.Element",0];
elementDI = JavaNew["sun4v.qc.Element",1];
Show[GraphicsArray[{Graphics3D[mesh[elementHO],
PlotRange -> {{-1,1},{-1,1},{-1,1}}],
Graphics3D[mesh[elementDI],
PlotRange -> {{-1,1},{-1,1},{-1,1}}]}]];

Methods

setParameter[num, value] num = 0 or 1, 0 <= value <= 1. Changes the form of a polyhedron.

Usage:
elementHO@setParameter[1,0.5];
elementHO@setParameter[0,0.25];
elementDI@setParameter[1,0.5];
elementDI@setParameter[0,0.25];
Show[GraphicsArray[{Graphics3D[mesh[elementHO],
PlotRange -> {{-1,1},{-1,1},{-1,1}}],
Graphics3D[mesh[elementDI],
PlotRange -> {{-1,1},{-1,1},{-1,1}}]}]];

ReleaseJavaObject[elementHO,elementDI];
Clear[elementHO,elementDI];

Modeler

A utility class. It is needed for making a parquet cover.

Constructors

Modeler[type] type = HO or DI.

Usage:
modelerHO = JavaNew["sun4v.qc.Modeler",0];
modelerDI = JavaNew["sun4v.qc.Modeler",1];

Fields

element it is an Element instance.

Methods

getUnitDirection[] gives the value that is used for correct scaling by the setUnitDirection[] method of the Quarkhedron class.
getUnitDistance[] gives the value that is used as the third argument of the park[] method of the Parker class.

Parker

A utility class. It is needed for making a parquet cover.

Methods

park[vertices, faces, unitDistance] gives a list of the coordinates of the parquet elements. Check of concurrence of faces is not made.
park[vertices, faces, unitDistance, flag] if flag is True check of concurrence of faces is made. Conterminous faces are dropped.

Usage:
parquet[obj_,modeler_] := Module[{m,v,f,g},
m = mesh[modeler@element];
LoadJavaClass["sun4v.qc.Parker"];
obj@setUnitDirection[modeler@getUnitDirection[]];
v = obj@getVertices[];
AllowRaggedArrays[True];
f = obj@getFaces[];
g = Graphics3D[TranslateShape[m,#]& /@
sun4v`qc`Parker`park[v,f,modeler@getUnitDistance[]]];
AllowRaggedArrays[False]; g]

quarkhedronHO@resetValues[];
quarkhedronDI@resetValues[];
Show[GraphicsArray[{parquet[quarkhedronHO,modelerHO],
parquet[quarkhedronDI,modelerDI]}]];

element = modelerHO@element;
element@setParameter[0,1];
element = modelerDI@element;
element@setParameter[0,1];
Show[GraphicsArray[{parquet[quarkhedronHO,modelerHO],
parquet[quarkhedronDI,modelerDI]}]];

ReleaseJavaObject[quarkhedronHO,quarkhedronDI,modelerHO,modelerDI];
Clear[quarkhedronHO,quarkhedronDI,modelerHO,modelerDI,element];